「データを爆速で見つけたい。でも、新しいデータを追加する手間も最小限にしたい」
そんな、あちらを立てればこちらが立たずという「わがまま」な願い。コンピュータの世界において、これは長年エンジニアを悩ませてきた宿命的なトレードオフでした。データ構造の基本である「配列」を使い続ける限り、私たちは常にこのジレンマに直面することになります。
しかし、コンピュータ科学の歴史には、この絶望的な二律背反を鮮やかに、そして極めて巧妙に打ち破った発明が存在します。それこそが「二分探索木(にぶんたんさくき)」、別名「ふたまたニョキニョキ」です。
今回は、C言語で挫折した人も、Excelの並び替えにイライラしている事務職の方も、誰もが「なるほど!」と膝を打つ、データ構造の革命を解説します。チョムスキーの言語学から、コンピュータの特技「ランダムアクセス」の秘密まで、点と点が繋がる快感を体験してください。
配列の限界:なぜ「整列済み配列」はエンジニアを絶望させるのか
データ構造の議論において、避けて通れないのが「探索(見つける)」と「挿入(加える)」のコストです。
例えば、1万人のデータを身長順にきれいに並べた「整列済み配列」があるとします。ここに特定の1人を探しに行く場合、私たちは「二分探索」という手法を使えます。真ん中の人と比較して、大きければ右半分、小さければ左半分……と範囲を半分に絞り込んでいく。この「探索」は爆速です。1万件あっても、わずか14回程度の比較で目的のデータに辿り着けます。
しかし、問題は「挿入」です。ここに、新しく180cmの「水野さん」を割り込ませようとしたらどうなるでしょうか。
「新しくデータを挿入しようとすると、それ以降のデータをすべて1つずつ後ろにずらさなければならず、膨大な計算量が発生してしまいます。」
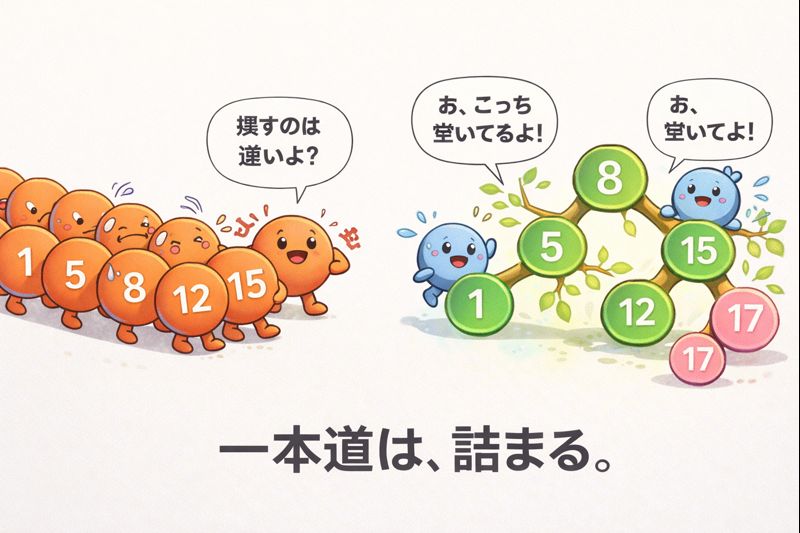
1万人いれば、最悪の場合1万個のデータを本棚の端から端までずるずるとずらして隙間を作る必要がある。これが、エンジニアが「オーダーN」と呼び、忌み嫌う「重さ」の正体です。データを1つ増やすたびに、システム全体が悲鳴を上げる。これが配列の抱える宿命的な限界なのです。
一方で、順番を気にせず最後尾にデータを放り込むだけの「無秩序な配列」は、挿入自体は一瞬(オーダー1)で終わりますが、探索は地獄です。端から順に1つずつ確認するしかなく、データが増えれば増えるほど「探しものが見つからない」というカオスに陥ります。
「探索が得意なものは挿入が苦手で、挿入が得意なものは探索が苦手。この2つを完全に凌駕するのが二分探索木なんです。」
「ふたまたニョキニョキ」参上!言語学とも共鳴するツリーの美学
この宿命を打ち破るために登場したのが、堀本さんが親しみやすく「ふたまたニョキニョキ」と命名した構造、すなわち「二分探索木」です。図に描くと、一つの場所から枝が二股に分かれ、それがさらに二股に分かれ……と、木が根を張るように、あるいは枝を広げるようにニョキニョキと伸びていく見た目をしています。
面白いことに、この「ツリー」という概念は、コンピュータ科学の専売特許ではありません。言語学の世界、特にチョムスキーの生成文法でも「ツリーダイアグラム」や「Xバー理論」として登場します。人間が言葉を紡ぐとき、心の中では単語が二股に分岐して、ある種の構造(分布)を形成している。そんな言語の深層構造と、コンピュータのデータ整理の理想形が「二股の分岐」という一点で重なるのは、決して偶然ではありません。
「分岐が止まった子供を左から見ていくと、全部綺麗に並んでいる。ちゃんと順番になっているし、探索もしやすいんです。」
二分探索木は、データの背後に「見えない木」を育てることで、配列のような「ずらす手間」を一切必要としない、全く新しい秩序を生み出したのです。
「右は大きく、左は小さい」という黄金律。なぜ二股だけで速くなるのか?
二分探索木のルールは、拍子抜けするほどシンプルです。
「自分より大きい値は右下へ、小さい値は左下へ」。ただこれだけを繰り返します。
例えば、最初に178cmの「水野さん」が頂点(ルート)にいるとします。
次に168cmの「堀本さん」を入れる場合、178より小さいので左下に吊るします。
さらに220cmの「チェ・ホンマン」が来れば、178より大きいので右下に吊るします。
もし185cmの人が新しく加わるなら、まず頂点の水野さん(178cm)と比較して「右」へ行き、次にそこにいるチェ・ホンマン(220cm)と比較して「左」に行く、というステップで場所が決まります。
この仕組みのすごいところは、探索と挿入が「同じプロセス」で完了することです。探索するときは、大小のルールに従って枝を下っていくだけ。挿入するときも、同じように枝を下っていき、空いている場所にピタッと吸着させるだけです。
配列のようにデータを「ずらす」必要は一切ありません。新しい枝を一本ニョキッと生やす。その一瞬の動作で、データ構造の美しさが保たれるのです。まさに、挿入が得意で探索も得意。配列が泣いて謝るほどの革命的な「いいとこ取り」と言えるでしょう。
爆速の秘密「ポインタ」と「ランダムアクセス」。コンピュータの特技を活かしきれ
「でも、メモリ上でデータを『斜め下』に吊るすなんて、どうやってるの?」
そう疑問に思ったあなたは鋭いです。コンピュータのメモリは、住所(番地)が割り振られた箱が一直線に並んでいるだけで、物理的に枝分かれしているわけではありません。
ここで活きるのは、コンピュータの圧倒的な特技「ランダムアクセス」です。これは「指定された番地に、どこであっても一瞬で飛べる」という能力です。
この能力を極限まで引き出す道具が、多くのプログラミング学習者が挫折する「ポインタ」です。ポインタとは、要するに「地図のメモ書き」です。
1つのデータの中に「次は168番地を見てね(左の子)」「あっちの250番地を見てね(右の子)」というメモ(番地)を書いておくのです。すると、コンピュータは「次は左だな」と判断した瞬間に、そのメモにある番地へワープするように飛んでいきます。
「ページ数をメモしておけばコンピューターはランダムアクセスできるから、そのページに一瞬で飛べる。だから便利なんです。」
ポインタは、メモリという一直線の空間を、縦横無尽にワープできる「魔法の道」に変えます。この「吊るしの技術」があるからこそ、私たちは物理的な配置を気にせず、論理的なツリー構造を爆速で扱うことができるのです。
最初の一手で運命が決まる。個性豊かなツリーの「光と影」
二分探索木の非常に人間味あふれる点は、「データの挿入順序によって、完成する木の形がダイナミックに変化する」ことです。
誰を最初に頂点(ルート)にするか。その次に誰をピックアップするか。それだけで、木が左右にバランスよく広がる「優等生」な形になることもあれば、ひょろひょろと片方にだけ伸びてしまう「個性派」な形になることもあります。
ここで正直なところ、この魔法には一つだけ「弱点」があります。
例えば「1, 2, 3, 4, 5…」と完璧に整列した順にデータを入れてしまうと、木は枝分かれせず、ただの長い一本棒になってしまいます。こうなると、せっかくの二分探索木も、ただの「クソ重い配列」と変わらなくなってしまうのです。
「運命は最初の一手で決まる」。この不確実性が、二分探索木の面白いところでもあります。現場のエンジニアたちは、この「ひょろひょろ問題」を解決するために、木が伸びるたびに自分で自分を組み直す「自己バランス木」という、さらに変態的なまでに巧妙な知恵を積み重ねてきました。
一見無機質なデータ構造の裏側には、コンピュータの物理的制約を数学的トリックで逆転させようとした、先人たちの執念とドラマが詰まっているのです。
まとめ
この記事をまとめると…
- トレードオフを殺す: 配列が抱えていた「探索速度」と「挿入負荷」の二律背反を、二分探索木は「二股の分岐」によって鮮やかに解決する。
- 黄金律の美学: 「大きい方は右、小さい方は左」という、言語学とも共通するシンプルなルールだけで、世界に秩序をもたらす。
- ポインタの真価: コンピュータの「ランダムアクセス」能力をポインタという「地図のメモ」で活かすことで、物理的な移動なしにデータを爆速で「吊るす」ことが可能になる。
- 動的な面白さ: 挿入順序によって木の形が変化する不確実性がある。この個性を制御しようとする挑戦こそが、コンピュータ科学の深淵である。
実際のところ、二分探索木を初めて学んだとき、私は「なんて性格の出る構造なんだ」と驚きました。効率を求めたはずの数学的な世界に、これほどドラマチックな仕組みが潜んでいる。
次にあなたが何かの検索ボタンを押したとき、その裏側で誰かが育てた「ふたまたニョキニョキ」が、あなたのために一瞬でワープを繰り返している様子を想像してみてください。きっと、無機質な画面が少しだけ愛おしく見えるはずです。
配信元
番組名:ゆるコンピュータ科学ラジオ
タイトル:巧妙なアイデア「ふたまたニョキニョキ」がすべてを解決する【データ構造2】#49
配信日:2022-12-04